-
 +25 +1
+25 +1How a magician-mathematician revealed a casino loophole
When a gang of gambling cheats sussed out how to beat the house, they inadvertently highlighted a loophole from a shuffled deck. It took a magician-turned-mathematician to reveal how.
-
 +22 +1
+22 +1Swiss university claims it broke the record for Pi calculation
Most people know the value of Pi as 3.1416, but it's gotten longer and longer over the years as researchers try to find its most accurate calculation. A team from the University of Applied Sciences Graubünden in Switzerland now claims it has broken the world record for computing for the mathematical constant: It said it has calculated for 62.8 trillion digits of Pi. The current record holder, Timothy Mullican, calculated up to 50 trillion digits and was recognized for his work last year.
-
 +4 +1
+4 +1AI maths whiz creates tough new problems for humans to solve
Algorithm named after mathematician Srinivasa Ramanujan suggests interesting formulae, some of which are difficult to prove true.
-
 +14 +1
+14 +1Math Genius Has Come Up With a Wildly Simple New Way to Solve Quadratic Equations
If you studied algebra in high school (or you're learning it right now), there's a good chance you're familiar with the quadratic formula. If not, it's possible you repressed it.
-
 +23 +1
+23 +1Why you might be counting in the wrong language
Learning numbers in a European language has probably affected your early maths ability. It turns out there are better ways to count.
-
 +3 +1
+3 +1Maths tackles an eternal question: where to park?
Two strategies for choosing a parking spot save far more time than a third, according to researchers’ estimates.
-
 +3 +1
+3 +1New Proof Settles Ancient Question of How to Approximate Numbers Like Pi
The ancient Greeks wondered when “irrational” numbers can be approximated by fractions. By proving the longstanding Duffin-Schaeffer conjecture, two mathematicians have provided a complete answer.
-
 +7 +1
+7 +1Unpacking The Math Problem That’s Dividing The Internet
BEDMAS, BODMAS or PEMDAS? Which do you use?
-
 +16 +1
+16 +1Couple wins millions using lottery loophole
It was completely legal and it won them millions. Jon Wertheim reports on how Jerry Selbee and his wife Marge used "basic arithmetic" to crack the code on certain lottery games
-
 +30 +1
+30 +1We've found a quicker way to multiply really big numbers
To multiply two numbers by hand take a few steps but it's something we're taught in school. When dealing with big numbers, really big numbers, we need to a quicker way to do things.
-
 +41 +1
+41 +1Mathematicians have found a new way to multiply two numbers together
The multiplication you learn at school is too slow for computers, so mathematicians are always searching for better methods.
-
 +17 +1
+17 +1‘Maths anxiety’ causing fear and despair in children as young as six
Children as young as six feel fear, rage and despair as a result of “mathematics anxiety”, a condition which can cause physical symptoms and behaviour problems in class, according to a study. Pupils in both primary and secondary school can find themselves locked in a cycle of despair, suffering from anxiety which harms their maths performance, which in turn leads to increased anxiety.
-
 +2 +1
+2 +1How Using Third-Grade Math Can Improve Your Life
If 9-year-old you could master basic math functions, then present-day you can certainly use them to take back your time and improve your life.
-
 +15 +1
+15 +1An anonymous 4chan post could help solve a 25-year-old math mystery
A 4chan poster may have solved part of a very tricky math problem that mathematicians have been working on for at least 25 years. The user was just trying to figure out the most efficient way to watch episodes of a nonlinear anime series, but the result has generated considerable interest from mathematicians around the world who have no way to identify the anonymous user.
-
 +14 +1
+14 +1How to Get Better at 'Back of the Envelope' Calculations
The art of estimations is pretty much a physicist's bread and butter. We all love a good estimation problem. You might also hear these called a "back of the envelope" calculation, or a calculation on a napkin. The writing medium is meant to emphasize how little preparation goes into attacking the problem. The estimator can't even take the time to find a clean sheet of paper.
-
 +2 +1
+2 +1Prime Numbers And Crystal-Like Materials Share A Hidden Organization
As it turns out, prime numbers and crystals have a lot in common. A new analysis from researchers at Princeton University suggests that the patterned distribution of prime numbers in the number line is remarkably similar to patterns found in the atomic structure of certain crystal-like materials. In simple terms, the sequence of primes over long stretches of the number line shows properties remarkably similar to the sequence that arises from shining X-rays on an object to reveal its internal atomic structure.
-
 +45 +1
+45 +1What Knitting Can Teach You About Math
In this professor's class, there are no calculators. Instead, students learn advanced math by drawing pictures, playing with beach balls—and knitting
-
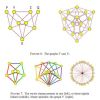 +7 +1
+7 +160-year-old maths problem partly solved by amateur
An amateur mathematician has made the first breakthrough in more than 60 years towards solving a well-known maths problem. Aubrey de Grey, who is more widely known as a maverick biologist intent on extending the human lifespan, has taken the academic world by surprise after announcing a new solution to the so-called Hadwiger-Nelson problem.
-
 +22 +1
+22 +1100 Prisoners Escape Puzzle
Recently, I wrote about a classic prisoner escape puzzle which, at first glance, appeared impossible. There’s another classic, impossible sounding, prisoner escape puzzle called the 100 prisoner problem. It was first written about by Danish computer scientist Peter Bro Miltersen. In this puzzle there are 100 prisoners, each given a distinct number 1-100. The jailer has decided to give all the prisoners a chance to escape. He prepares a challenge, and if every single one of the prisoners passes, they are all free to go. If even one of them fails, they all die.
-
 +1 +1
+1 +1Stop celebrating Pi Day, and embrace Tau as the true circle constant
Pi Day is a lie day
Submit a link
Start a discussion




















